线性模型
家族

Linear Model Family

从基础线性回归到高级正则化技术的完整探索之旅

开始探索 实践项目
y = θ₀ + θ₁x
σ(z) = 1/(1+e⁻ᶻ)
J(θ) = ½Σ(h-y)²

模型全景

From Simple to Complex: A Journey Through Linear Models

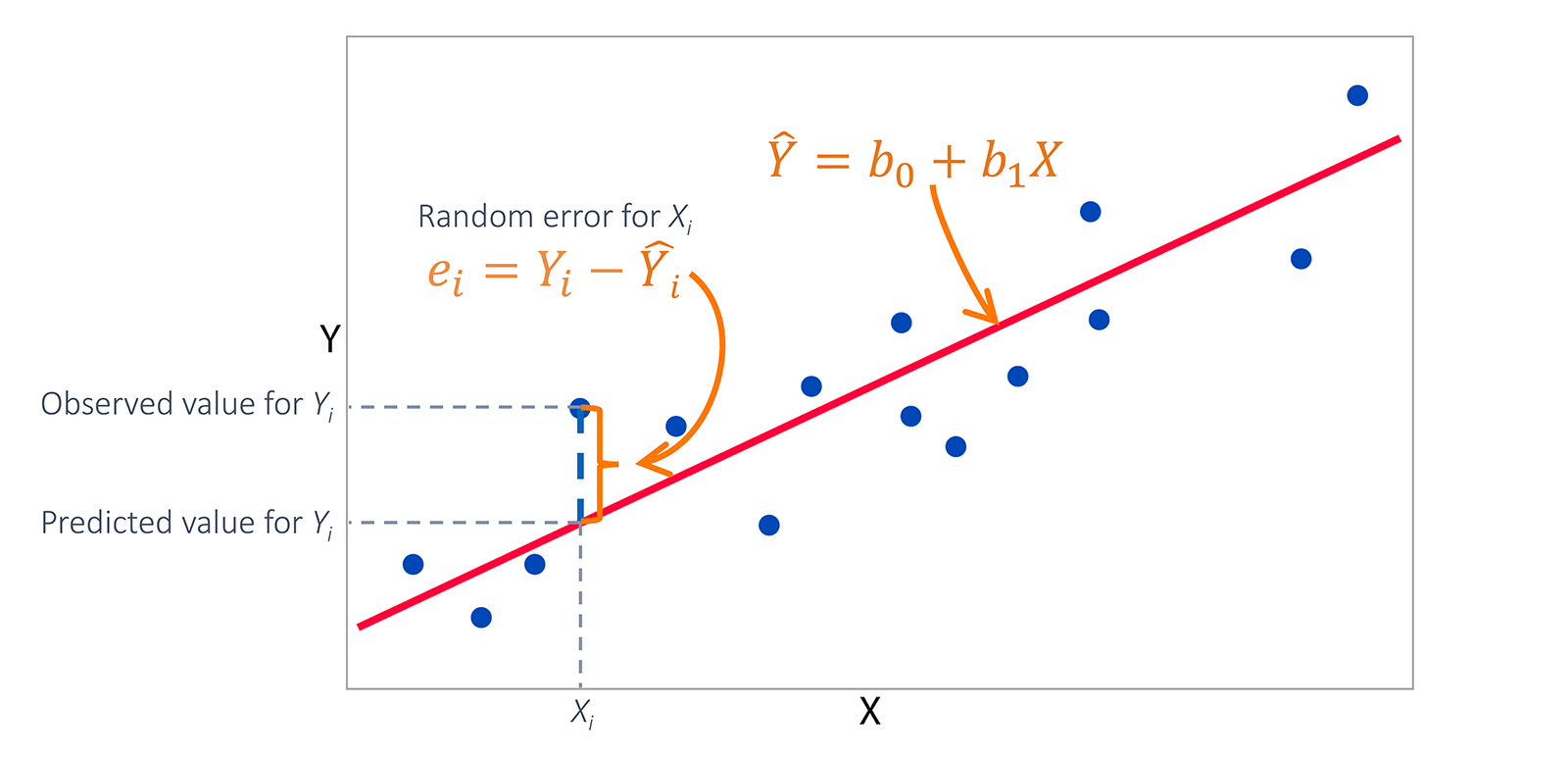
线性回归

Linear Regression

最小二乘法寻找最佳拟合直线，通过最小化预测值与实际值之间的平方误差来确定模型参数。

核心公式

y = θ₀ + θ₁x₁ + ... + θₙxₙ

损失函数

J(θ) = ½m⁻¹Σ(hθ(x)-y)²
Linear Regression Visualization

逻辑回归

Logistic Regression

通过Sigmoid函数将线性输出映射到概率空间，解决分类问题。

梯度下降

Gradient Descent

迭代优化算法，通过计算梯度方向逐步找到损失函数的最小值。

岭回归

Ridge Regression (L2 Regularization)

添加L2正则化项防止过拟合，通过惩罚大的参数值来提高模型的泛化能力。

J(θ) = MSE + λΣθ²

Lasso & 弹性网络

L1 Regularization & Elastic Net

Lasso通过L1正则化实现特征选择，弹性网络结合L1和L2的优势。

Lasso:

J(θ) = MSE + λΣ|θ|

Elastic Net:

J(θ) = MSE + λ₁Σ|θ| + λ₂Σθ²

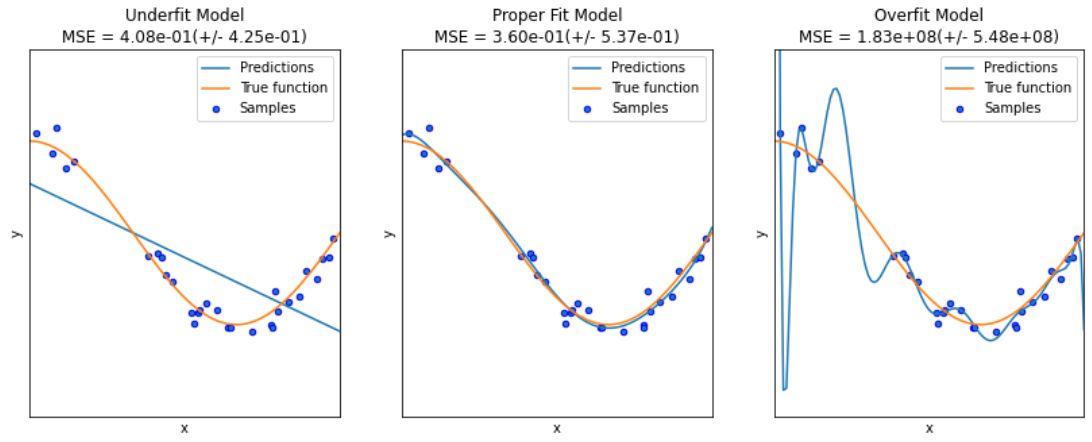
模型对比

Model Comparison

特征选择
解释性
抗过拟合

可视化演示

Interactive Visualizations & Algorithm Demos

Sigmoid 函数

Sigmoid Function

Sigmoid函数将任意实数映射到(0,1)区间，是逻辑回归的核心激活函数。

σ(z) = 1 / (1 + e^(-z))

梯度下降过程

Gradient Descent Animation

可视化展示梯度下降算法如何逐步找到损失函数的最小值点。

θ = θ - α∇J(θ)

正则化对比

Regularization Comparison

岭回归 (L2)

收缩所有系数，不进行特征选择，适合处理多重共线性。

λΣθ²

Lasso (L1)

将不重要特征系数设为零，实现自动特征选择。

λΣ|θ|

弹性网络

结合L1和L2优势，在特征选择和稳定性间平衡。

λ₁Σ|θ| + λ₂Σθ²

性能对比

Model Performance Comparison

回归模型性能指标

分类模型性能指标

特征重要性对比

实践项目

Hands-on Projects: From Theory to Practice

房价预测项目

House Price Prediction

数据探索与可视化分析
特征工程与数据预处理
模型训练与正则化选择
性能评估与结果解释

技术栈

Python Scikit-learn Pandas Matplotlib

预期成果

MAE < 20K, R² > 0.85

客户流失预测

Customer Churn Prediction

客户行为数据分析
类别不平衡处理
逻辑回归模型构建
业务洞察与决策建议

关键指标

92%

准确率

0.89

AUC值

商业价值

降低流失率 15%

实现指南

手写实现

从零开始实现线性回归和逻辑回归，深入理解算法原理和数学推导过程。

工程实践

使用Scikit-learn构建完整的机器学习流水线，包含特征工程和模型评估。

可视化分析

创建交互式可视化图表，展示模型性能、特征重要性和决策边界。